E Data Frame Wrangling in R

E.1 Creating Data Frames

Most frequently, we will be creating data frames based on a series of numeric, logical, characters vectors of identical lengths.

x <- data.frame(
    u=runif(5),
    v=sample(c(TRUE, FALSE), 5, replace=TRUE),
    w=LETTERS[1:5]
)
print(x)

##          u     v w
## 1 0.181517  TRUE A
## 2 0.919723 FALSE B
## 3 0.311723 FALSE C
## 4 0.064152  TRUE D
## 5 0.396422 FALSE E

Some objects, such as matrices, can easily be coerced to data frames:

(A <- matrix(1:12, byrow=TRUE, nrow=3,
    dimnames=list(
        NULL,     # row labels
        c("x", "y", "z", "w") # column labels
)))

##      x  y  z  w
## [1,] 1  2  3  4
## [2,] 5  6  7  8
## [3,] 9 10 11 12

as.data.frame(A)

##   x  y  z  w
## 1 1  2  3  4
## 2 5  6  7  8
## 3 9 10 11 12

Named lists are amongst other candidates for a meaningful conversion:

(l <- lapply(split(iris$Sepal.Length, iris$Species),
    function(x) {
        c(min=min(x), median=median(x), mean=mean(x), max=max(x))
    }))

## $setosa
##    min median   mean    max 
##  4.300  5.000  5.006  5.800 
## 
## $versicolor
##    min median   mean    max 
##  4.900  5.900  5.936  7.000 
## 
## $virginica
##    min median   mean    max 
##  4.900  6.500  6.588  7.900

as.data.frame(l)

##        setosa versicolor virginica
## min     4.300      4.900     4.900
## median  5.000      5.900     6.500
## mean    5.006      5.936     6.588
## max     5.800      7.000     7.900

E.2 Importing Data Frames

Many interesting data frames come from external sources, such as CSV files, web APIs, SQL databases and so on.

In particular, read.csv() (see ?read.table for a long list of tunable parameters) imports data from plain text files organised in a tabular manner (such as comma-separated lists of values):

f <- tempfile() # temporary file name
write.csv(x, f, row.names=FALSE) # save data frame to file
cat(readLines(f), sep="\n") # print file contents

## "u","v","w"
## 0.181517061544582,TRUE,"A"
## 0.919722604798153,FALSE,"B"
## 0.31172346835956,FALSE,"C"
## 0.0641516039613634,TRUE,"D"
## 0.396421572659165,FALSE,"E"

read.csv(f)

##          u     v w
## 1 0.181517  TRUE A
## 2 0.919723 FALSE B
## 3 0.311723 FALSE C
## 4 0.064152  TRUE D
## 5 0.396422 FALSE E

Note that CSV is by far the most portable format for exchanging matrix-like objects between different programs (statistical or numeric computing environments, spreadsheets etc.).

E.3 Data Frame Subsetting

class(x)

## [1] "data.frame"

typeof(x)

## [1] "list"

length(x) # number of columns

## [1] 3

names(x)  # column labels

## [1] "u" "v" "w"

x$u # accessing column `u` (synonym: x[["u"]])

## [1] 0.181517 0.919723 0.311723 0.064152 0.396422

x[[2]] # 2nd column

## [1]  TRUE FALSE FALSE  TRUE FALSE

x[c(1,3)] # a sub-data.frame

##          u w
## 1 0.181517 A
## 2 0.919723 B
## 3 0.311723 C
## 4 0.064152 D
## 5 0.396422 E

sapply(x, class) # apply class() on each column

##           u           v           w 
##   "numeric"   "logical" "character"

dim(x) # number of rows and columns

## [1] 5 3

x[1:2,] # first two rows

##         u     v w
## 1 0.18152  TRUE A
## 2 0.91972 FALSE B

x[,c(1,3)] # 1st and 3rd column, synonym: x[c(1,3)]

##          u w
## 1 0.181517 A
## 2 0.919723 B
## 3 0.311723 C
## 4 0.064152 D
## 5 0.396422 E

x[,1] # synonym: x[[1]]

## [1] 0.181517 0.919723 0.311723 0.064152 0.396422

x[,1,drop=FALSE] # synonym: x[1]

##          u
## 1 0.181517
## 2 0.919723
## 3 0.311723
## 4 0.064152
## 5 0.396422

x[x$u>=0.3 & x$u<=0.6, ]

##         u     v w
## 3 0.31172 FALSE C
## 5 0.39642 FALSE E

x[!(x[,"u"]<0.3 | x[,"u"]>0.6), ] # equivalent

##         u     v w
## 3 0.31172 FALSE C
## 5 0.39642 FALSE E

(x_sorted <- x[order(x$u),])

##          u     v w
## 4 0.064152  TRUE D
## 1 0.181517  TRUE A
## 3 0.311723 FALSE C
## 5 0.396422 FALSE E
## 2 0.919723 FALSE B

row.names(x_sorted) <- NULL
x_sorted

##          u     v w
## 1 0.064152  TRUE D
## 2 0.181517  TRUE A
## 3 0.311723 FALSE C
## 4 0.396422 FALSE E
## 5 0.919723 FALSE B

E.4 Common Operations

We already know how to filter rows based on logical conditions, e.g.:

iris[iris$Petal.Width >= 1.2 & iris$Petal.Width <= 1.3,
    c("Petal.Width", "Species")]

##     Petal.Width    Species
## 54          1.3 versicolor
## 56          1.3 versicolor
## 59          1.3 versicolor
## 65          1.3 versicolor
## 72          1.3 versicolor
## 74          1.2 versicolor
## 75          1.3 versicolor
## 83          1.2 versicolor
## 88          1.3 versicolor
## 89          1.3 versicolor
## 90          1.3 versicolor
## 91          1.2 versicolor
## 93          1.2 versicolor
## 95          1.3 versicolor
## 96          1.2 versicolor
## 97          1.3 versicolor
## 98          1.3 versicolor
## 100         1.3 versicolor

iris[iris$Sepal.Length > 6.5 & iris$Species == "versicolor", ]

##    Sepal.Length Sepal.Width Petal.Length Petal.Width    Species
## 51          7.0         3.2          4.7         1.4 versicolor
## 53          6.9         3.1          4.9         1.5 versicolor
## 59          6.6         2.9          4.6         1.3 versicolor
## 66          6.7         3.1          4.4         1.4 versicolor
## 76          6.6         3.0          4.4         1.4 versicolor
## 77          6.8         2.8          4.8         1.4 versicolor
## 78          6.7         3.0          5.0         1.7 versicolor
## 87          6.7         3.1          4.7         1.5 versicolor

and aggregate information in individual columns:

sapply(iris[1:4], summary)

##         Sepal.Length Sepal.Width Petal.Length Petal.Width
## Min.          4.3000      2.0000        1.000      0.1000
## 1st Qu.       5.1000      2.8000        1.600      0.3000
## Median        5.8000      3.0000        4.350      1.3000
## Mean          5.8433      3.0573        3.758      1.1993
## 3rd Qu.       6.4000      3.3000        5.100      1.8000
## Max.          7.9000      4.4000        6.900      2.5000

Quite frequently, we will be interested in summarising data within subgroups generated by a list of factor-like variables.

aggregate(iris[1:4], iris[5], mean)  # not: iris[, 5] !

##      Species Sepal.Length Sepal.Width Petal.Length Petal.Width
## 1     setosa        5.006       3.428        1.462       0.246
## 2 versicolor        5.936       2.770        4.260       1.326
## 3  virginica        6.588       2.974        5.552       2.026

ToothGrowth[sample(nrow(ToothGrowth), 5), ] # 5 random rows

##     len supp dose
## 12 16.5   VC  1.0
## 10  7.0   VC  0.5
## 17 13.6   VC  1.0
## 50 27.3   OJ  1.0
## 60 23.0   OJ  2.0

aggregate(ToothGrowth["len"], ToothGrowth[c("supp", "dose")], median)

##   supp dose   len
## 1   OJ  0.5 12.25
## 2   VC  0.5  7.15
## 3   OJ  1.0 23.45
## 4   VC  1.0 16.50
## 5   OJ  2.0 25.95
## 6   VC  2.0 25.95

According to the manual of the aggregate function, see help("aggregate"), the syntax is aggregate(x, by, FUN), where:

• x is a data frame whose columns are to be aggregated;
• by is a list of grouping elements, each as long as the variables in the data frame x; recall that each data frame is a list of vectors of identical lengths, so ultimately this can also be a data frame as well; this is why we have written iris[5] and neither iris[[5]] nor iris[, 5] (although we could have used the iris[, 5, drop=FALSE] notation);
• FUN is an R function to be applied on each column in x within all groups of observations defined by by.

Further arguments can be passed to the function being called, e.g., using the notation like aggregate(X, y, mean, na.rm=TRUE).

ToothGrowth["supp"]  # selects a specific column from a data frame; the result is still a data frame; remember that a data frame is also a list
ToothGrowth[["supp"]] # this is different - this is a vector; cannot be used in aggregate, at least not as `by` argument; extracts data from a column, is no longer a data frame
ToothGrowth[c("supp", "dose")]  # selects 2 columns
aggregate(ToothGrowth["len"], ToothGrowth["supp"], mean)  # computing average len in groups defined by supp
aggregate(ToothGrowth["len"], ToothGrowth[c("supp", "dose")], mean)  # computing average len in groups defined by combinations of supp and dose
f <- function(x) c(MEAN=mean(x), MEDIAN=median(x))  # a custom function that returns two aggregates in form of a named (labelled) vector
aggregate(ToothGrowth["len"], ToothGrowth["supp"], f)
aggregate(ToothGrowth["len"], ToothGrowth[c("supp", "dose")], f)

ToothGrowth[["dose_1_or_2"]] <- ToothGrowth[["dose"]] >= 1.0  # note 2 square brackets now - dealing with individual columns
ToothGrowth  # note the added column
aggregate(ToothGrowth["len"], ToothGrowth["dose_1_or_2"], function(x) c(MIN=min(x), MAX=max(x)))

Taking into account that split() accepts a data frame input as well, we can perform what follows:

sapply(
    # split iris into 3 sub-data.frames:
    split(iris, iris[5]),
    # on each sub-data.frame, apply the following function
    function(df) {
        # compute the mean of first four columns:
        sapply(df[1:4], mean)
    })

##              setosa versicolor virginica
## Sepal.Length  5.006      5.936     6.588
## Sepal.Width   3.428      2.770     2.974
## Petal.Length  1.462      4.260     5.552
## Petal.Width   0.246      1.326     2.026

sapply(split(iris, iris[5]), function(df) {
    c(Sepal.Length=summary(iris$Sepal.Length),
      Petal.Length=summary(iris$Petal.Length)
     )
})

##                      setosa versicolor virginica
## Sepal.Length.Min.    4.3000     4.3000    4.3000
## Sepal.Length.1st Qu. 5.1000     5.1000    5.1000
## Sepal.Length.Median  5.8000     5.8000    5.8000
## Sepal.Length.Mean    5.8433     5.8433    5.8433
## Sepal.Length.3rd Qu. 6.4000     6.4000    6.4000
## Sepal.Length.Max.    7.9000     7.9000    7.9000
## Petal.Length.Min.    1.0000     1.0000    1.0000
## Petal.Length.1st Qu. 1.6000     1.6000    1.6000
## Petal.Length.Median  4.3500     4.3500    4.3500
## Petal.Length.Mean    3.7580     3.7580    3.7580
## Petal.Length.3rd Qu. 5.1000     5.1000    5.1000
## Petal.Length.Max.    6.9000     6.9000    6.9000

The above syntax solely relies on the building blocks that we have already mastered! This should be very appealing to the minimalists.

Note that R packages data.table and dplyr provide us with reimplementations of the most important functions for the processing of data frames. We ​only cover the classic/base functions here, because they have existed since the very beginning of R. These are known to every R user and are likely to work this way forever. Having said this, we should acknowledge that some users might find dplyr or data.table more convenient (oftentimes they are faster or handle big data better) in many contexts. The problem, though, is that when faced with less typical problems (as a future AI/ML engineer/data scientist we’ll be particularly exposed to them), we’ll have to fall back to base R anyway, because it is more powerful and gives us more transferable skills (also with regards to objects of different types, e.g., matrices). This is exactly why we prefer functions like aggregate() subsetting like df[,], etc.

E.5 Metaprogramming and Formulas (*)

R (together with a few other programming languages such as Lisp and Scheme, that heavily inspired R’s semantics) allows its programmers to apply some metaprogramming techniques, that is, to write programs that manipulate unevaluated R expressions.

For instance, take a close look at the following plot:

z <- seq(-2*pi, 2*pi, length.out=101)
plot(z, sin(z), type="l")

Figure E.1: Metaprogramming in action: Just take a look at the Y axis label

How did the plot() function know that we are plotting sin of z (see Figure E.1)? It turns out that, at any time, we not only have access to the value of an object (such as the result of evaluating sin(z), which is a vector of 101 reals) but also to the expression that was passed as a function’s argument itself.

test_meta <- function(x) {
    cat("x equals to ", x, "\n") # \n == newline
    cat("x stemmed from ", deparse(substitute(x)), "\n")
}
test_meta(2+7)

## x equals to  9 
## x stemmed from  2 + 7

This is very powerful and yet potentially very confusing to the users, because we can write functions that don’t compute the arguments provided in a way we expect them to (i.e., following the R language specification). Each function can constitute a new micro-verse, where with its own rules – we should always refer to the documentation.

For instance, consider the subset() function:

head(iris)

##   Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 1          5.1         3.5          1.4         0.2  setosa
## 2          4.9         3.0          1.4         0.2  setosa
## 3          4.7         3.2          1.3         0.2  setosa
## 4          4.6         3.1          1.5         0.2  setosa
## 5          5.0         3.6          1.4         0.2  setosa
## 6          5.4         3.9          1.7         0.4  setosa

subset(iris, Sepal.Length>7.5, select=-(Sepal.Width:Petal.Width))

##     Sepal.Length   Species
## 106          7.6 virginica
## 118          7.7 virginica
## 119          7.7 virginica
## 123          7.7 virginica
## 132          7.9 virginica
## 136          7.7 virginica

Neither Sepal.Length>6 nor -(Sepal.Width:Petal.Width) make sense as standalone R expressions! However, according to the subset() function’s own rules, the former expression is considered as a row selector (here, Sepal.Length refers to a particular column within the iris data frame). The latter plays the role of a column filter (select everything but all the columns between…).

The data.table and dplyr packages (which are very popular) rely on this language feature all the time, so we shouldn’t be surprised when we see them.

There is one more interesting language feature that is possible thanks to metaprogramming. Formulas are special R objects that consist of two unevaluated R expressions separated by a tilde (~). For example:

len ~ supp+dose

## len ~ supp + dose

A formula on its own has no meaning. However, many R functions accept formulas as arguments and can interpret them in various different ways.

For example, the lm() function that fits a linear regression model, uses formulas to specify the output and input variables:

lm(Sepal.Length~Petal.Length+Sepal.Width, data=iris)

## 
## Call:
## lm(formula = Sepal.Length ~ Petal.Length + Sepal.Width, data = iris)
## 
## Coefficients:
##  (Intercept)  Petal.Length   Sepal.Width  
##        2.249         0.472         0.596

On the other hand, boxplot() (see Figure E.2) allows for creating separate box-and-whisker plots for each subgroup given by a combination of factors.

boxplot(len~supp+dose, data=ToothGrowth,
    horizontal=TRUE, col="white")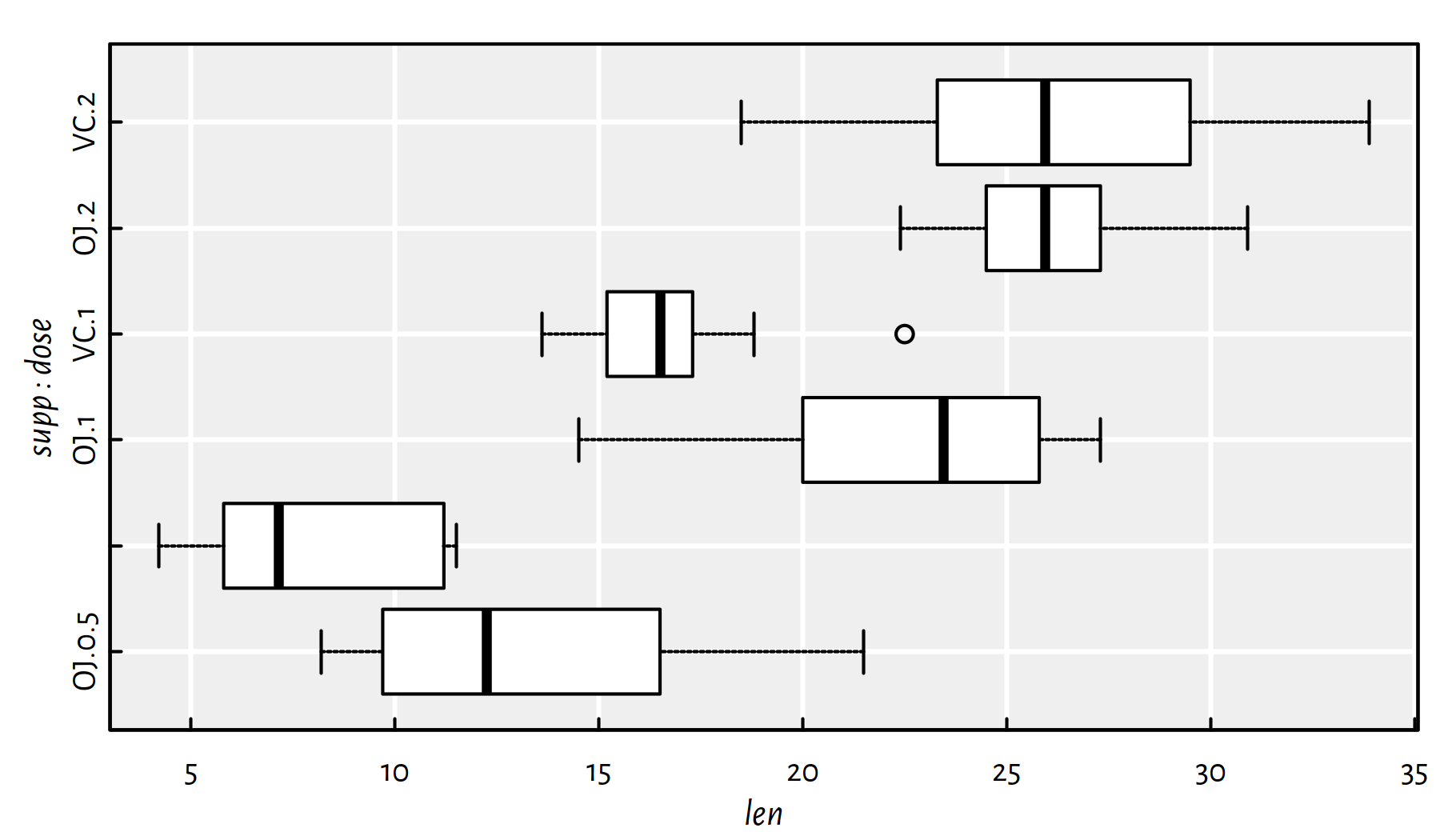

Figure E.2: Example box plot created via the formula interface

The aggregate() function supports formulas too:

aggregate(cbind(Sepal.Length, Sepal.Width)~Species, data=iris, mean)

##      Species Sepal.Length Sepal.Width
## 1     setosa        5.006       3.428
## 2 versicolor        5.936       2.770
## 3  virginica        6.588       2.974

We should therefore make sure that we know how every function interacts with a formula – information on that can be found in ?lm, ?boxplot, ?aggregate and so forth.

E.6 Further Reading

Recommended further reading: (Venables et al. 2021)

Other: (Peng 2019), (Wickham & Grolemund 2017)

R packages dplyr and data.table implement the most common data frame wrangling procedures. You may find them very useful. Moreover, they are very fast even for large data sets. Additionally, the magrittr package provides a pipe operator, %>%, that simplifies the writing of complex, nested function calls. Do note that not everyone is a big fan of these, however.